IT310 Java Support Site
Today is: 2025-04-26 | Current Unit: 02
- Newsletters
- Seminar Agendas and Recordings
- Project Instructions and Demos
- Tutorials, Tips, and Tricks
- Submit a Help Ticket
 |
|||||||||
| A newsletter published by http://java.skillbuilderblocks.com to help students succeed! | |||||||||
| Course: IT310 Data Structures and Algorithms | Vol: 1301C | Issue: 1 | Date: 2013-02-28 | |||||||||
|
|||||||||
 |
|||||||||||||||
| A newsletter published by http://java.skillbuilderblocks.com to help students succeed! | |||||||||||||||
| Course: IT310 Data Structures and Algorithms | Vol: 1301C | Issue: 2 | Date: 2013-03-07 | |||||||||||||||
|
|||||||||||||||
 |
|||||||||
| A newsletter published by http://java.skillbuilderblocks.com to help students succeed! | |||||||||
| Course: IT310 Data Structures and Algorithms | Vol: 1301C | Issue: 3 | Date: 2013-03-14 | |||||||||
|
|||||||||
 |
|||||||||
| A newsletter published by http://java.skillbuilderblocks.com to help students succeed! | |||||||||
| Course: IT310 Data Structures and Algorithms | Vol: 1301C | Issue: 4 | Date: 2013-03-28 | |||||||||
|
|||||||||
 |
|||||||||
| A newsletter published by http://java.skillbuilderblocks.com to help students succeed! | |||||||||
| Course: IT310 Data Structures and Algorithms | Vol: 1301C | Issue: 5 | Date: 2013-04-04 | |||||||||
|
|||||||||
 |
|||||||||
| A newsletter published by http://java.skillbuilderblocks.com to help students succeed! | |||||||||
| Course: IT310 Data Structures and Algorithms | Vol: 1301C | Issue: 6 | Date: 2013-04-11 | |||||||||
|
|||||||||
 |
|||||||||
| A newsletter published by http://java.skillbuilderblocks.com to help students succeed! | |||||||||
| Course: IT310 Data Structures and Algorithms | Vol: 1301C | Issue: 7 | Date: 2013-04-18 | |||||||||
|
|||||||||
 |
|||||||||
| A newsletter published by http://java.skillbuilderblocks.com to help students succeed! | |||||||||
| Course: IT310 Data Structures and Algorithms | Vol: 1104C | Issue: 8 | Date: 10-12-2011 | |||||||||
|
|||||||||
 |
|||||||||
| A newsletter published by http://java.skillbuilderblocks.com to help students succeed! | |||||||||
| Course: IT310 Data Structures and Algorithms | Vol: 1301C | Issue: 9 | Date: 2013-05-02 | |||||||||
|
|||||||||
 |
|||||||||
| A newsletter published by http://java.skillbuilderblocks.com to help students succeed! | |||||||||
| Course: IT310 Data Structures and Algorithms | Vol: 1301C | Issue: 10 | Date: 2013-05-09 | |||||||||
|
|||||||||
The seminar recording covering the following topics is here http://khe2.adobeconnect.com/p2bp4y7lw4g/
- Introductions and survey on programming knowledge
- What I expect from you
- Understand the syllabus
- Do the assigned readings
- Practice, practice, practice
- Read my announcements
- Do the work and participate!
- Have fun!!!!!
- What you can expect from me
- Timely communication
- Comprehensive grade feedback
- Information packed seminars
- Lots of support!
- Fun!!!
- How to Get help
- Virtual Office (I look there first and frequently)
- The Java support site
- KUO Technology Center - link under Course Home
- Introduction to Java and Object Oriented Programming (OOP)
- What is Java?
- What can it do - or what can you do with it?
- What is OOP?
- This week's goal
- Download and install the JDK and IDE
- Submit a screenshot of your successful execution of the test.java program
- Project Demo
The seminar recording covering the following topics is here http://khe2.adobeconnect.com/p1f34ski7m7/
- What is an algorithm?
- A precise description of the steps needed in a computation that produces a solution to a problem
- The sequence of instructions within a program that implements a processing operation
- A problem-solving procedure that uses comparison and branching functions
- Algorithmic complexity analysis
- Review newsletter for scope
- The differences between the best, worst, and average case for an algorithm
- Best case is when the algorithm can do the job in the fewest number of steps
- Worst case is when the algorithm does the job in the greatest number of steps
- Average case falls between best and worst, but is problematic because you would have to know all possibilities and probabilities to determine average
- Example: A sequential search of an unordered array finds the value in the first cell (best case); it finds the value in the last cell or not at all (worst case); Calculating average
- An efficient algorithm
- Generally speaking a program with the best running time is a better one
- For programs that run only once or a few times and are no longer needed, any algorithm will do except for exponential (quadratic, cubic, etc) - they may never finish
- This week's goal - demo (see project instructions for more details)
- Modify Time.java by adding methods for n^2 and 2^n and functions that output the results.
- Run the program
- Copy and paste the outputted data into Excel. Graph the time data and modify the graph as needed.
- Save the Excel file in the unit02 folder, zip it and attach it to the dropbox.
The seminar recording covering the following topics is here http://khe2.adobeconnect.com/p3hvowlrevb/
- Linked Lists
- Singly linked lists
- A linked structureis a collection of nodes storing data and links to other nodes
- Alinked listis a data structure composed of nodes, each node holding some information and a reference to another node in the list
- A singly linked listis a node that has a link only to its successor in this sequence
- Doubly linked lists
- A doubly linked list is when each node in a linked list has two reference fields, one to the successor and one to the predecessor
- Circular lists
- A circular listis when nodes form a ring: The list is finite and each node has a successor
- Skip lists
- A skip list is a variant of the ordered linked list that makes a nonsequential search possible
- In a skip list of n nodes, for each k and i such that 1 <= k <= [lg n] and 1 <= i <= [n/2k - 1] -1, the node in position 2k - 1 - i points to the node in position 2k - 1 - (i+ 1)
- The number of reference fields indicates the level of each node, and the number of levels is maxLevel= [lg n] + 1
- Self-organizing lists - ordering methods
- Move-to-front method - after the desired element is located, put it at the beginning of the list
- Transpose method - after the desired element is located, swap it with its predecessor unless it is at the head of the list
- Count method - order the list by the number of times elements are being accessed
- Ordering method - order the list using certain criteria natural for the information under scrutiny
- Optimal static ordering - all the data are already ordered by the frequency of their occurrence in the body of data so that the list is used only for searching, not for inserting new items
- Sparse tables
- A sparse tablerefers to a table that is populated sparsely by data and most of its cells are empty
- With a sparse table, the table can be replaced by a system of linked lists
- This week's goal - demo (see project instructions for more details)
The seminar recording covering the following topics is here http://khe2.adobeconnect.com/p4o28te9bck/
- Common Abstract Data Structures
- Stacks
- void push (int newItem) - Add newItem to top of stack.
- int pop() - Remove the top int from the stack and return it.
- Queues
- Recursion
- This week's goal - demo (see project instructions for more details)
A stack consists of a sequence of items, which should be thought of as piled one on top of the other like a physical stack of boxes or cafeteria trays. Only the top item on the stack is accessible at any given time. It can be removed from the stack with an operation called pop. An item lower down on the stack can only be removed after all the items on top of it have been popped off the stack. A new item can be added to the top of the stack with an operation called push. We can make a stack of any type of items. If, for example, the items are values of type int, then the push and pop operations can be implemented as instance methods
Note that a stack can be implemented either as a linked list or ordered array, though there is a risk of the push operation to result in worst case run time analysis in the case the array is full.
Queues are similar to stacks in that a queue consists of a sequence of items, and there are restrictions about how items can be added to and removed from the list. However, a queue has two ends, called the front and the back of the queue. Items are always added to the queue at the back and removed from the queue at the front. The operations of adding and removing items are called enqueue and dequeue. An item that is added to the back of the queue will remain on the queue until all the items in front of it have been removed. This should sound familiar. A queue is like a "line" or "queue" of customers waiting for service. Customers are serviced in the order in which they arrive on the queue.
A queue can be implemented as a linked list or as an array. An efficient array implementation is a little trickier than the array implementation of a stack.
The seminar recording covering the following topics is here http://khe2.adobeconnect.com/p8r618qnr80/
- Binary trees and traversals
- Binary search trees an heaps
- This week's goal - demo (see project instructions for more details)
Each of the objects in a binary tree contains two pointers, typically called left and right. In addition to these pointers, of course, the nodes can contain other types of data. For example, a binary tree of integers could be made up of objects of the following type: class TreeNode { int item; // The data in this node. TreeNode left; // Pointer to the left subtree. TreeNode right; // Pointer to the right subtree. } The left and right pointers in a TreeNode can be null or can point to other objects of type TreeNode. A node that points to another node is said to be the parent of that node, and the node it points to is called a child.
The most common traversal uses a depth-first approach and include preorder, postorder and inorder methods. In a preorder traversal, the root node of the tree is processed first, then the left subtree is traversed, then the right subtree. In a postorder traversal , the left subtree is traversed, then the right subtree, and then the root node is processed. And in an inorder traversal , the left subtree is traversed first, then the root node is processed, then the right subtree is traversed.
Searching and inserting are efficient operations on a binary search tree, provided that the tree is close to being balanced. A binary tree is balanced if for each node, the left subtree of that node contains approximately the same number of nodes as the right subtree. In a perfectly balanced tree, the two numbers differ by at most one. Not all binary trees are balanced, but if the tree is created by inserting items in a random order, there is a high probability that the tree is approximately balanced. (If the order of insertion is not random, however, it’s quite possible for the tree to be very unbalanced.) During a search of any binary sort tree, every comparison eliminates one of two subtrees from further consideration. If the tree is balanced, that means cutting the number of items still under consideration in half. This is exactly the same as the binary search algorithm, and the result is a similarly efficient algorithm.
A heap is a special portion of memory where objects are stored. Instead of holding an object itself, a variable holds the information necessary to find the object in memory. This information is called a reference or pointer to the object. In effect, a reference to an object is the address of the memory location where the object is stored. When you use a variable of object type, the computer uses the reference in the variable to find the actual object.
The seminar recording covering the following topics is here http://khe2.adobeconnect.com/p7jkfvv0plt/
- Calculating Shortest Route (Dijkstra's Algorithm)
- Here is a good resource for understanding the algorithm interactively: http://www-b2.is.tokushima-u.ac.jp/~ikeda/suuri/dijkstra/DijkstraApp.shtml?demo7
- This week's goal - demo (see project instructions for more details)
The seminar recording covering the following topics is here http://khe2.adobeconnect.com/p8dcd0k9eq3/
- Sorting Algorithms
- Elementary Algorithms
- Insertion
- Good for small data sets
- Not as efficient as quicksort, heapsort or mergesort
- Sorts an array as it receives it
- Similar to how humans sort
- Selection
- Not as efficient as insertion sort
- Finds minimum value, swaps it with the first position and repeats to second postion, and so on
- Bubble
- Analogous to how small elements "bubble" up to the top of a list
- Not as efficient as insertion sort
- Compares adjacent items and swaps them if they're in wrong order
- Efficient Algorithms
- Shell
- Heap
- Quick
- Merge
- Radix
- This week's goal - demo (see project instructions for more details)
The seminar recording covering the following topics is here http://khe2.adobeconnect.com/p93ko7fvpf3/
- Preliminaries
- Only one more seminar after tonight!
- Here is a great resource you should investigate: http://math.hws.edu/eck/cs124/javanotes6/
- This week's topic: Hashing - go here for basic understanding of Java implementation: http://javarevisited.blogspot.com/2011/02/how-hashmap-works-in-java.html
- This week's goal - demo (see project instructions for more details)
The seminar recording covering the following topics is here http://khe2.adobeconnect.com/p3nwmyz3wz8/
- Preliminaries
- Last seminar!
- Final projects are due no later than 05-15-2013.
- Unit 9 suggested topics (please email me for approval if you have another topic you would like to explore):
- Social networking
- Security of the Internet
- How technology can help you learn
- Privacy and security of cell phones
- Technology and your major
- The best ways to learn new technology
- How to protect yourself from identity theft
- Video game addiction
- Do games help students learn?
- What is open source?
- Web 2.0: What is it, and why is it different?
- How has technology affected families?
- Twitter and Facebook in business today
- Online shopping—benefits and hazards
- How and why to do a podcast
- Search engine optimization (SEO)
- Cybercrime
- Computer forensics
- Disaster recovery plans
- Technology and a career (real estate, sales person, manager, teacher, pastor, nonprofit, funeral director, etc.)
- What influence has videoconferencing made on business, medicine, education, and social lives?
- How will Internet2 improve access to information?
- Final project
- Part A: Design, develop, and document an application used in business or academic setting
- A few examples include an order entry system, a simple transportation logistics system for finding the shortest/quickest routes, a network topology, game or tutorial. Use at least three data structures such as a linked list, stack, queue, tree, or graph. In a Word document, create a technical document explaining the program functions and data structures.
- Part B: Write a sypnopsis of what you have learned in this course
- Describe how you will use the knowledge in other classes, in your career or personally
- Explain why the knowledge is important
- Demo of example projects (no code demos - you're on your own!)
- Part A: Design, develop, and document an application used in business or academic setting
PROJECT INSTRUCTIONS
Install the JDK and your choice of an IDE
From the website http://www.oracle.com/technetwork/java/javase/downloads/index.html you will download the latest copy of the JDK software. I recommend downloading the JDK and NetBeans package. Be sure to choose the correct version for your platform (32 or 64-bit). The download location should be noted. When the download is complete you will double click on the file to install it.
Upon completion of the installation, launch NetBeans (or other IDE). You are now ready to start developing projects
Test your installation
Go to Doc Sharing in the classroom and download the file test.java and save it in a unit01 folder. Create a new project in your IDE. Choose java project with existing sources. Include the folder containing the test.java file. Compile and run the project. Create a screenshot using ctrl-print screen or the snipping tool if you have Windows 7 of your results. See the screenshot for Unit 1 below.
Directions for Submitting Your Project- Zip the file/folder that contains your screenshot. Note if you used html, you must include the html page and the image for the image to display on my end.
- Go to the Dropbox by clicking on the Dropbox tab above.
PROJECT DEMO
SCREEN SHOT OF SUCCESSFUL INSTALLATION
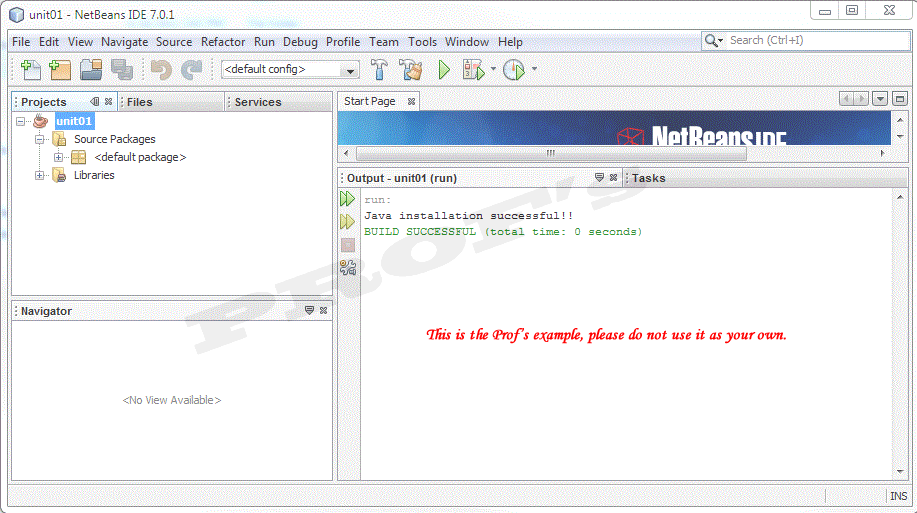
PROJECT INSTRUCTIONS
Calculate Squares, Exponentials, Run Times and Graph the Time Results
- Download Time.java from Doc Sharing and save it in a folder named unit02
- Create a new project in your IDE named unit02. Choose java project with existing sources. Include the folder containing the Time.java file
- Modify the timing program by adding two methods, one called squared that calculates and prints n2, and one called exponential that calculates and prints 2n
- Compile and run the project
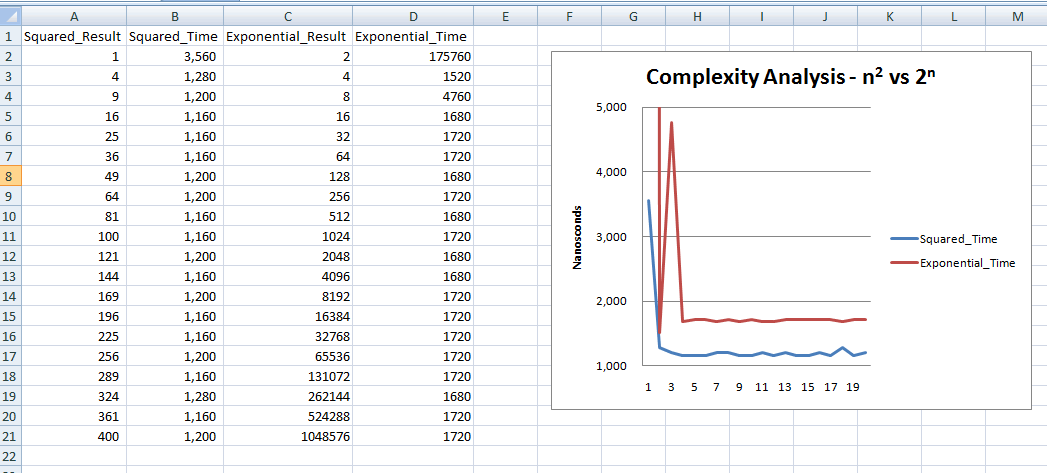
- Copy and paste the output into Excel (use text to columns if necessary to make the data graphable)
- Graph the time for each execution of the square and exponential loops
- Modify the graph to make the data readable if necessary
- Save the Excel file as unit02.xlsx in your unit02 compiled project folder
- Zip the unit02 project folder and attach the zip to the dropbox
PROJECT DEMO
SCREEN SHOT OF NETBEANS OUTPUT
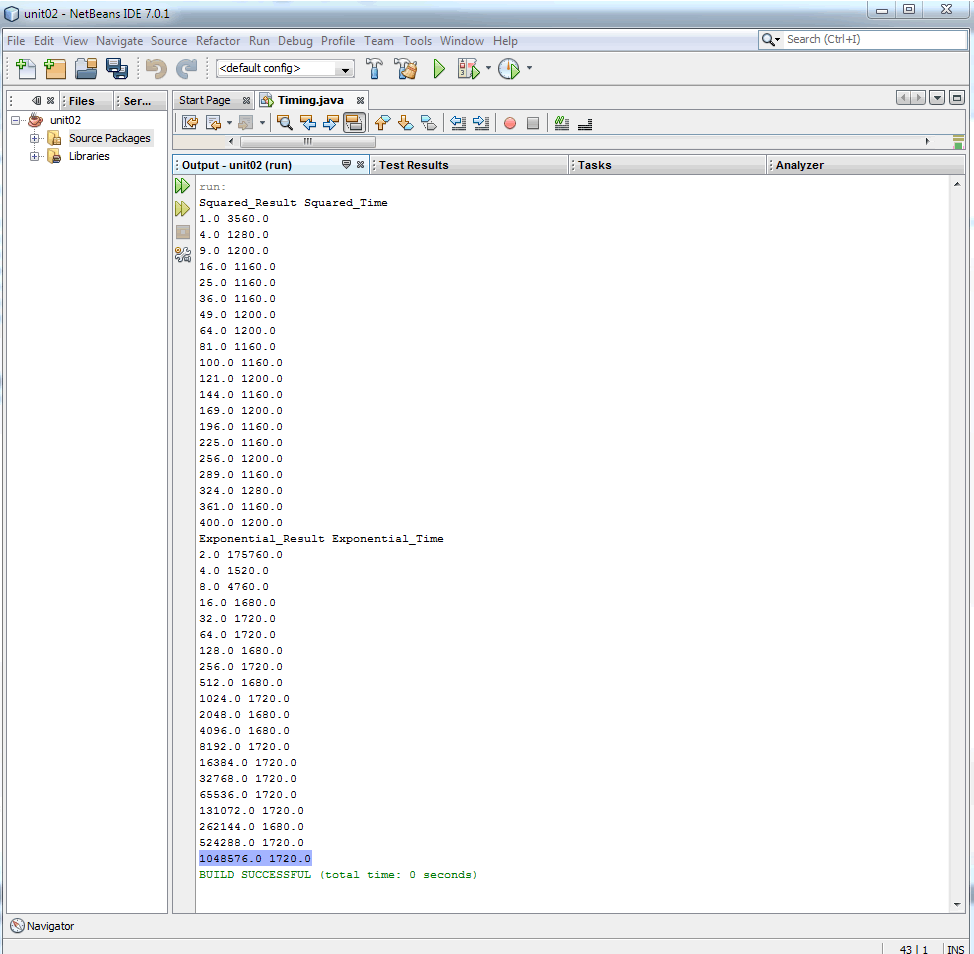
SCREEN SHOT OF EXCEL DATA AND GRAPH
PROJECT INSTRUCTIONS
Create an airline program that uses linked lists
Write an airline ticket reservation program called airline.java. The program should display a menu with the following options:
- Enter a flight in the schedule
- Check available flights
- Check reservations (display passengers)
- Reserve a ticket
- Cancel a reservation
- Check whether a ticket is reserved for a particular person
The information is maintained on an alphabetized linked list of names. Assume that tickets are reserved for only one flight. Create a linked list of flights with each node including a reference to a linked list of passengers.
PROJECT DEMO
SCREEN SHOT OF NETBEANS OUTPUT
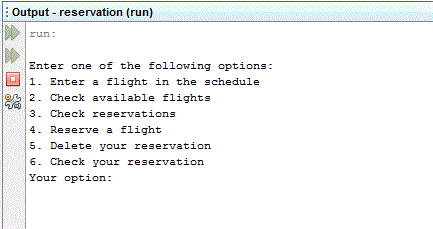
PROJECT INSTRUCTIONS
Travel Distances
Create a Java program that prompts the user to enter five cities and the x and y coordinates for each city (latitude and longitude). After all cities have been entered, the program should use a recursive algorithm to print the length of all possible routes that start at the first city entered and end at the last city For each route, the program should print the name of each city visited, followed by the length of the route.
Note: The distance between two points (x1, y1) and (x2, y2) is: Distance = or ((x2 – x1)˛ + (y2 – y1)2)1/2
PROJECT DEMO
SCREEN SHOT OF NETBEANS OUTPUT
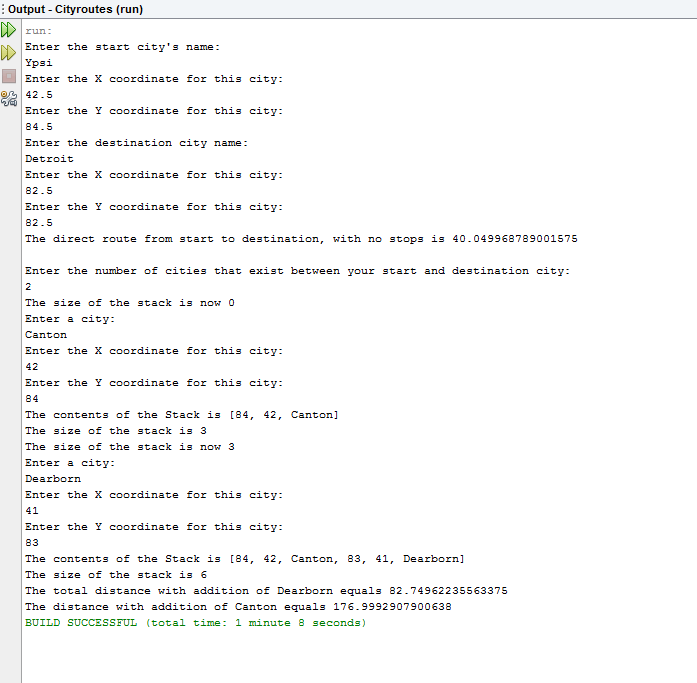
PROJECT INSTRUCTIONS
Fitness Club Membership
Create a ClubMember class that represents a member of a fitness club. Use a binary tree to store a set of club members based on their membership ID number. Display the membership ID along with the name of the club members.
PROJECT DEMO
SCREEN SHOT OF NETBEANS OUTPUT
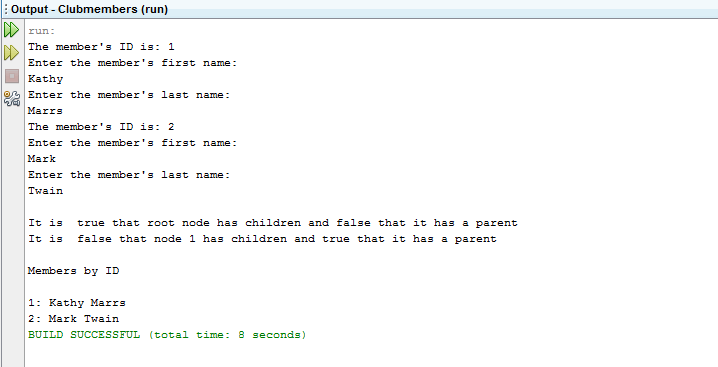
PROJECT INSTRUCTIONS
Using Dijkstra's Algorithm to Calculate the Shortest Path
Create a transportation logistics system that allows a user to enter a city to city connection and the prices shortest route given that the departure city may or may not have a direct route to the chosen destination (adjacency). Your system should [allow a user to enter two cities and] return the shortest path and the cheapest path between the two cities (NOTE: This has been changed because in this context the terms cost/price refer to resources - the shortest is the least "expensive" in terms of system requirements). Use a directed weighted graph. You may use Dijkstra’s Algorithm or another algorithm available on the Internet or in your text for calculating the shortest path.
Special Treat
In this week's seminar demo I'll show you some basic Swing techniques so you can begin creating GUI projects!
PROJECT DEMO
SCREEN SHOT OF NETBEANS OUTPUT
Download the graph pic here.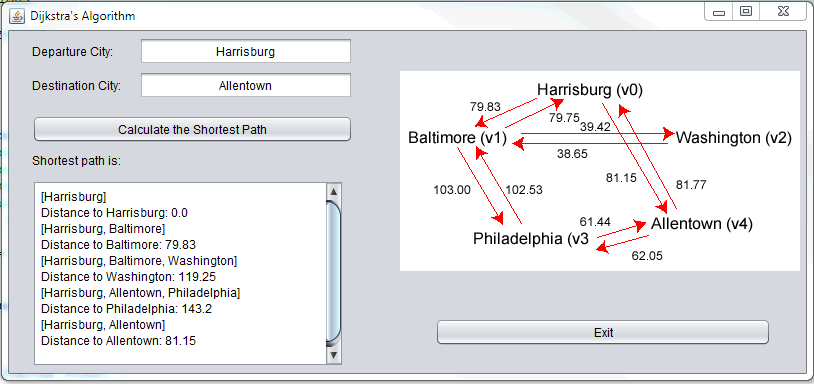
PROJECT INSTRUCTIONS
Using Sorting Algorithms
Modify the sorting algorithms located in doc sharing (selection sort, insertion sort, bubble sort, quick sort, and merge sort) by adding code to each to tally the total number of comparisons and total execution time of each algorithm. Execute the sort algorithm against the same list, recording information for the total number of comparisons and total execution time for each algorithm. Try several different lists. Record your results in the table in the attached document.
In a Word document, summarize your analysis of the sorting algorithms along with the tables. Submit the Word document and the modified sorting algorithms in a zip file.
PROJECT DEMO
SCREEN SHOT OF NETBEANS OUTPUT
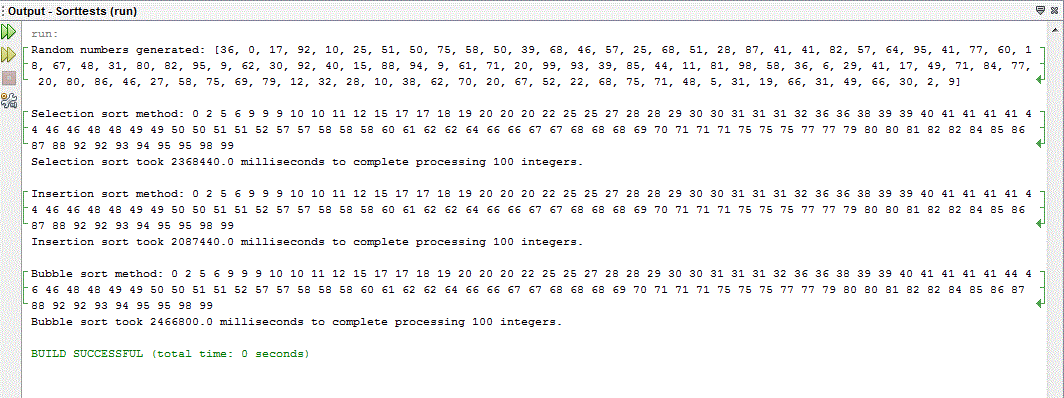
PROJECT INSTRUCTIONS
Using Hashing Algorithms
Write a program that inserts records into a hash table and retrieves and deletes them using either extendible hashing or the linear hashing (probing) technique. You may use a Java console or GUI application.
PROJECT DEMO
SCREEN SHOT OF NETBEANS OUTPUT
The following is the output of a non-generic implementation of a hash table. Note that you only need methods for put, get, remove, and exit. You will need the TextIO.java class to get it to work.
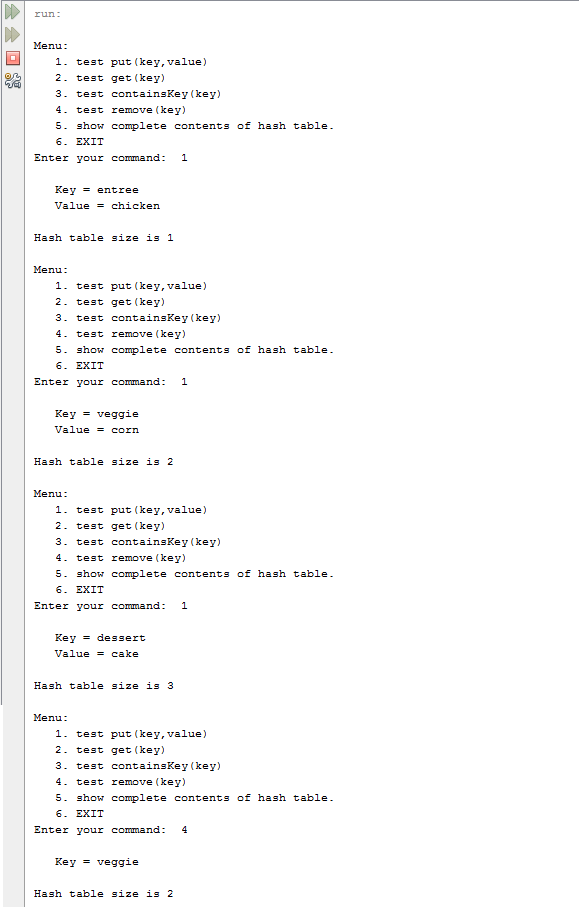
SCREEN SHOTS OF CUSTOM METHODS
Note, I have excluded the methods for menu option 5 and menu option 3, so don't forget when you code your main method to exclude them in your menu!
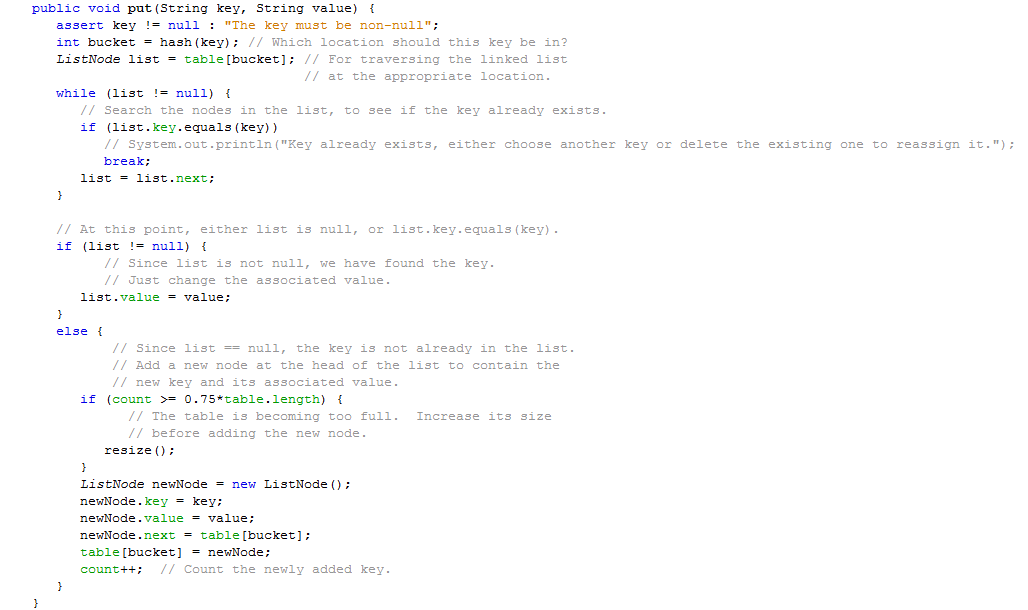

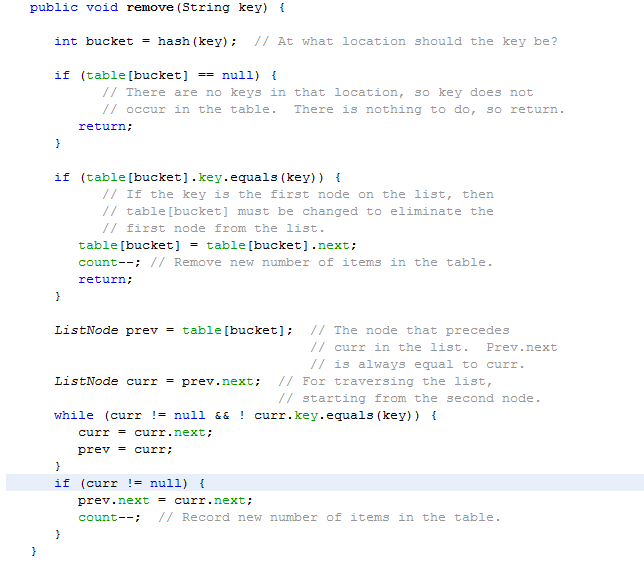

PROJECT INSTRUCTIONS
Unit 9: Research Project
Research the topic of human expressions within culture. You may use the Internet or other sources. Choose a topic that you find interesting and e-mail your professor for topic approval. After topic approval, prepare a two page paper in APA format summarizing your topic. Submit your paper as YourNameUnit9Project.docx.
Unit 10: Final Project
Part A:
Create an application to be used by a business. A few examples include an order entry system, a simple transportation logistics system for finding the shortest/quickest routes, or a network topology. Use at least three data structures such as a linked list, stack, queue, tree, or graph. In a Word document, create a technical document explaining the program functions and data structures.
Part B:
Based on the knowledge you have achieved thus far in our class, compose a brief synopsis compiling what you have learned about the data structures discussed in class. Describe how you will use this knowledge with any other class, your present or future career, or your own personal life. Be sure to also explain why you feel what has been learned in our class is important to you personally or professionally?
PROJECT DEMO
SCREEN SHOT OF NETBEANS OUTPUT
No screen shot for units 9 and 10. If you like, you may use the TextIO.java class for your final project.
PROJECT INSTRUCTIONS
Unit 10: Final Project
Part A:
Create an application to be used by a business. A few examples include an order entry system, a simple transportation logistics system for finding the shortest/quickest routes, or a network topology. Use at least three data structures such as a linked list, stack, queue, tree, or graph. In a Word document, create a technical document explaining the program functions and data structures.
Part B:
Based on the knowledge you have achieved thus far in our class, compose a brief synopsis compiling what you have learned about the data structures discussed in class. Describe how you will use this knowledge with any other class, your present or future career, or your own personal life. Be sure to also explain why you feel what has been learned in our class is important to you personally or professionally?
PROJECT DEMO
SCREEN SHOT OF NETBEANS OUTPUT
No screen shot for units 9 and 10. If you like, you may use the TextIO.java class for your final project.
Still not enough time! Hopefully sooner than later.
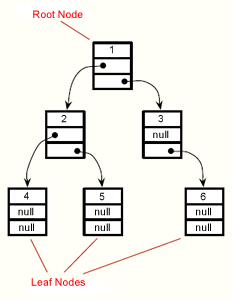 Previously you learned about linked data structures and abstract data types including stacks and queues. In this unit you'll learn about binary trees, which are more complex yet very useful linked structures. You can envision such a structure by picturing an upside down tree where the root is at the top and each node has two pointers that branch to other nodes or children. With the exception of the root, which has no parent, every other node has exactly one parent and a parent that has no children is a leaf.
Previously you learned about linked data structures and abstract data types including stacks and queues. In this unit you'll learn about binary trees, which are more complex yet very useful linked structures. You can envision such a structure by picturing an upside down tree where the root is at the top and each node has two pointers that branch to other nodes or children. With the exception of the root, which has no parent, every other node has exactly one parent and a parent that has no children is a leaf.